R语言十八讲(九):假设检验；(十):OLS回归

R语言十八讲(九)—假设检验

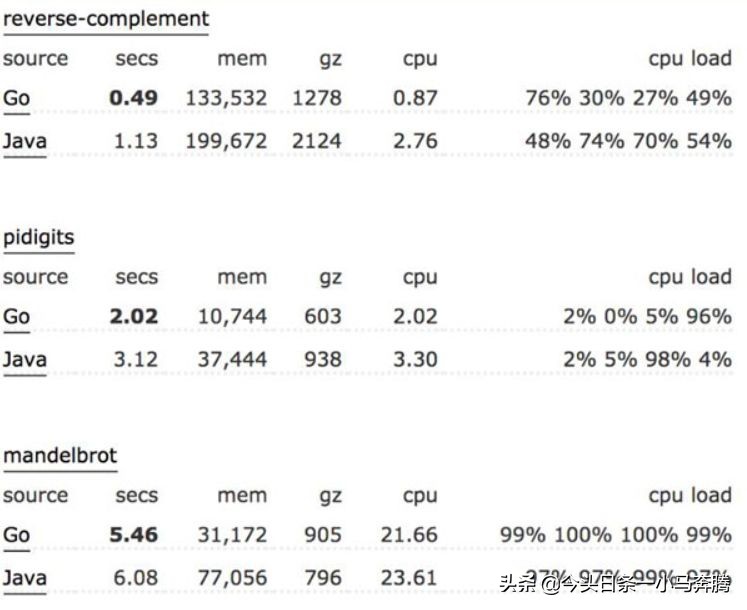
前面八章介绍了R软件的基础知识,这些知识都是零碎的操作与处理,虽然不能处理一个完整的实际案例,但却非常重要,接下来,主要讲数据挖掘中处理实际案例之前,所需要的一些模型和功能,我们先从传统的统计学开始,然后到数据挖掘算法,首先,我们会讲讲统计学中的基础知识模型,包括假设检验,线性回归,方差分析,等等.

1.检验

什么叫检验叻? 很简单就是去判断一件事的真伪,运用到统计学上就是去检验一个假设的真伪,去检验一个结论,一个说法的真伪.

数学原理:根据提出的假设,推导出一个理论性结果,然后与样本的实际观测结果相对比,若其差距超出了给定的范围,我们就认为假设不成立,也就是拒绝原假设,若其差距没有超出给定的范围,我们只是暂时接受假设,这里的的接受是指含有一点无奈的意思,即暂时还没有充分的证据推翻你的结论,而无奈接受结论,因为我们这里并没证明结论一定为真,只是通过这个模型没有推翻而已,这就是接受无奈,反对有理.在实际生活中也有很多这样的思想,比方疑罪从无的原则,即只要没有充分的证据证明我有罪,那么只能无奈的接受我没有罪.所以假设检验有一定的局限性,在运用时,原假设的设定非常有讲究..

具体操作;

例1:有两个样本数据,他们是独立的,且分别来自正太分布的总体,现在我们的问题就是去检验这两个样本所代表的总体的均值是否相等,在统计学中我们认为当然也可以证明两个独立样本的均值之差,经过标准化处理后,服从t分布,而t分布的概率密度分布图像跟正太分布是差不多的,现在我们假设两个总体均值相等,如果按照假设的来,那么两个样本均值之差及其标准化之后的数值应该是0或者0左右不远处吧(因为样本有随机性,),那么如果我们计算出的值距离0很远很远,这种事情发生的概率很小很小,但现在我们一次样本中就发生了,我们有理由相信根本不是我们中了彩票,一下子就碰到了这么小概率的事件,而是你给出的假设有问题,不是真实的.所以我们有理由拒绝给出的假设,从而推翻某一结论.

运用R的函数t.test(样本1数据,样本2数据) 就可以检验两个来自正太总体的独立样本.

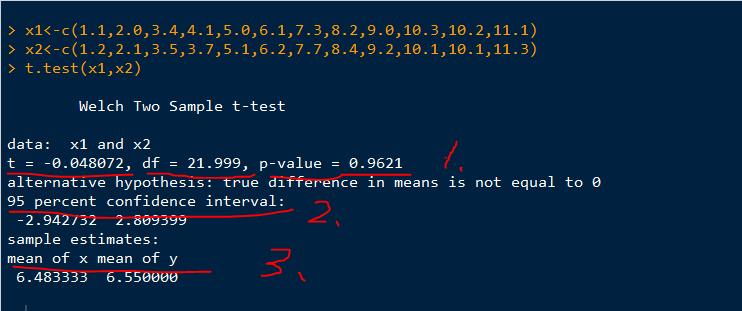
结果分析:画红线是我标上去的,1.分别是t检验量,自由度,和P值 2.95%的置信区间 3.两组数据的平均值

P值（P value）就是当原假设为真时所得到的样本观察结果或更极端结果出现的概率。如果P值很小，说明原假设情况的发生的概率很小，而如果出现了，根据小概率原理，我们就有理由拒绝原假设，P值越小，我们拒绝原假设的理由越充分。这里是0.96比较高,就接受原假设咯. t值在置信区间内我们就暂且相信原假设了..

而非独立样本则t.test(样本1数据,样本2数据,paired=T)

多于两组的样本我们用方差分析,这在以后会说到.

若不知道总体是否服从同一分布,但两组样本独立 则 wilcox.test( 样本1数据,样本2数据 )

若不知道总体是否服从同一分布,且两组样本不独立,则 wilcox.test( 样本1数据,样本2数据 ,paired=T )

例2.有一组数据,来自正太总体.现在检验其总体均值是否为某个数,比方100.那么原假设就是u=100,而在统计学上已经证明样本均值标准化后,服从相应的正太分布.那么我们就用Z分位检验就可以了.

总结:只要其服从什么分布,就用相应的统计量来检验就可以啦,.检验的根据就是,如果你的原假设为真,那么这件事情发生的概率我是可以根据样本实际观测值计算出来的,若得到的结果表明,这个事概率很小很小,比规定的还小,我们就有理由拒绝原假设,若其概率没有比规定的小,我们就暂且接受吧.

未完待续,

PPV原创文章,严禁转载. (文:@白加黑治感冒)

R语言十八讲(十)–OLS回归

前面讲到了假设检验,可以检验某个简单的结论,判断两个总体是否显著不同,今天,讲统计学中非常经典的一个知识,这就是回归,回归的分类很多,今天主要讲其中的OLS回归,OLS回归包括三大部分,分别是简单线性回归,多项式回归,多元线性回归.回归在数据分析中应用的非常广泛,可以做分类,也可以做预测,当然,更注重预测.接下来,我们讲讲回归的原理及流程.

一.简单线性回归

1.要解决的问题

简单线性回归是要找出一个变量与另一个变量的函数关系,这比相关分析更高一级,相关分析只能找出两个变量是否有线性关系,而线性回归则能找出具体的函数关系.

2.原理

简介:通过样本训练集的数据,运用最小二乘法,即根据拟合的理论值与实际观测值的误差最小化,来找出线性表达式的各个参数.

前提假设:待预测的变量y与自变量x具有线性关系,固定x则对应的y服从正太分布,每一y的值其分布的方差相同

那么,由此我们可以根据训练数据找到一条直线,它近似的表达了x与y的函数关系,其形式如同:y=ax+b,当然,由此式子计算出的y值,我们称之为理论值,它和y的实际观测值有一定的误差,我们把这个误差之和求出来,使之达到最小的情况下,对应的那个函数式子就是我们拟合的线性回归函数

3.操作

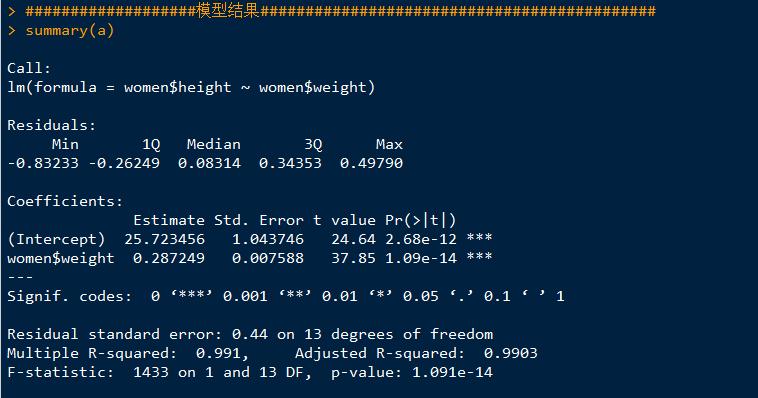
模型拟合:

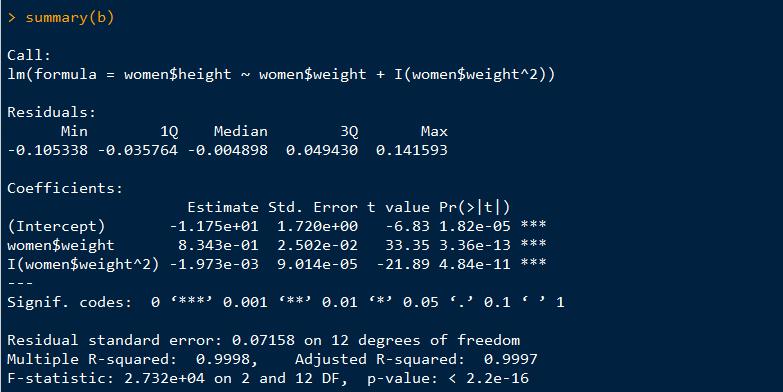
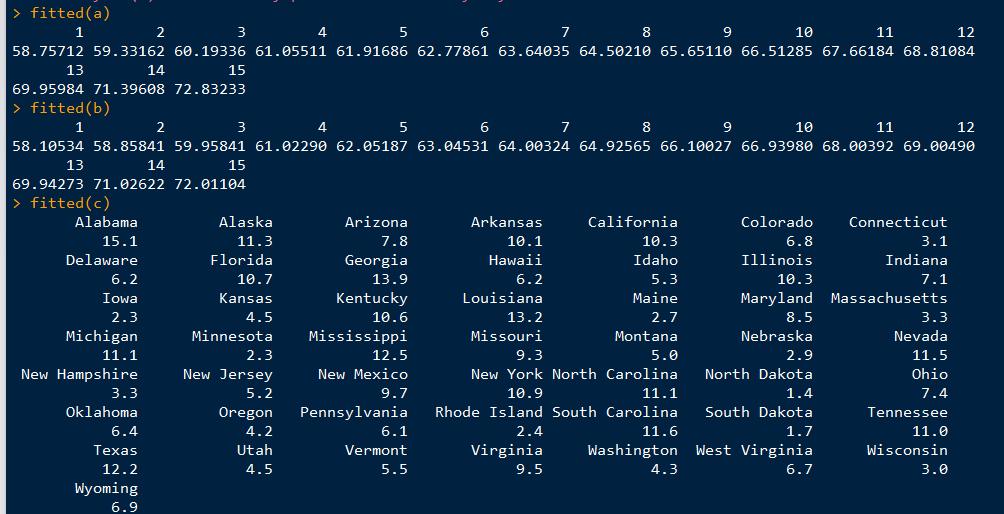
查看模型结果:其中residuals是残差,就是实际值与理论模拟值的误差,intercept是截距,后面的pr(>|t|)是p值,越小越拒绝原假设,结果越显著,还有adjusted R-squared表示模型拟合优度,越大越好.fitted即是通过模型拟合出的理论值.

模型可视化:

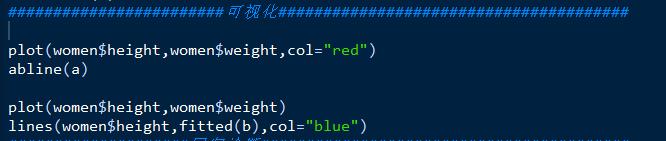
拓展:当自变量为多个时,这时未满需要拟合出一个函数,将y用几个自变量来表示,这在数据挖掘中还有另外一个作用,就是可以降维,将多属性多维数据降维1维,这样来避免维灾,这在以后也会讲到.

检验:由于我们是假设x和y服从一定条件下,推导出来的一些式子.那么,我们就需要来验证假设是否为真,当假设为真时,我们就承认推导出的式子有用,这时我们用可视化的方式来检验,当然数学中有公式可以检验,但是,比较复杂,我们不必了解,只需知道,当我们用R做假设验证的时候,出来的结果怎么样就可以通过,怎么样就不能通过,不能通过后,我们怎么修改模型即可.

这四幅图分别是1.残差拟合图(左上)

2.QQ图(右上)

3.位置比例图(左下)

4.残差杠杆图(右下)

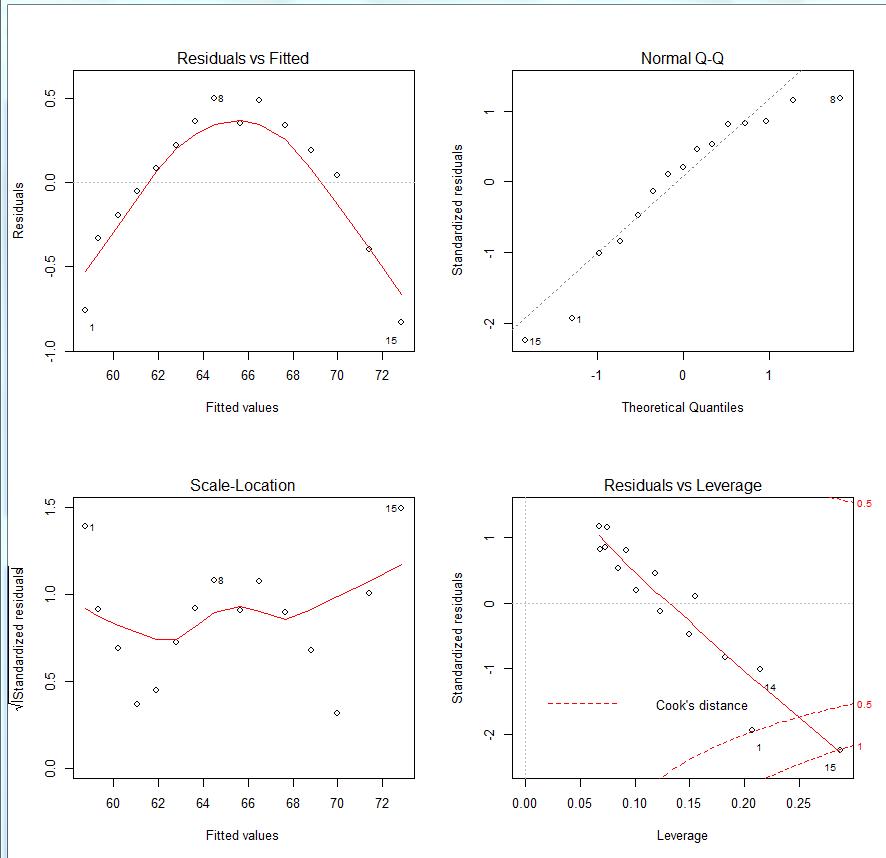
正态性 :当预测变量值固定时，因变量成正态分布，则残差值也应该是一个均值为0的正态分布。正态Q-Q图（Normal Q-Q，右上）是在正态分布对应的值下，标准化残差的概率图。若满足正态假设，那么图上的点应该落在呈45度角的直线上；若不是如此，那么就违反了正态性的假设。

 独立性: 你无法从这些图中分辨出因变量值是否相互独立，只能从收集的数据中来验证。上面的例子中，没有任何先验的理由去相信一位女性的体重会影响另外一位女性的体重。假若你发现数据是从一个家庭抽样得来的，那么可能必须要调整模型独立性的假设。

 线性 :若因变量与自变量线性相关，那么残差值与预测（拟合）值就没有任何系统关联。换句话说，除了白噪声，模型应该包含数据中所有的系统方差。在“残差图与拟合图”（Residuals vs Fitted，左上）中可以清楚的看到一个曲线关系，这暗示着你可能需要对回

归模型加上一个二次项。

 同方差性: 若满足不变方差假设，那么在位置尺度图（Scale-Location Graph，左下）中，水平线周围的点应该随机分布。该图似乎满足此假设。

最后一幅“残差与杠杆图”（Residuals vs Leverage，右下）提供了你可能关注的单个观测点的信息。从图形可以鉴别出离群点、高杠杆值点和强影响点。下面来详细介绍。

 一个观测点是离群点，表明拟合回归模型对其预测效果不佳（产生了巨大的或正或负的残差）。

 一个观测点有很高的杠杆值，表明它是一个异常的预测变量值的组合。也就是说，在预测变量空间中，它是一个离群点。因变量值不参与计算一个观测点的杠杆值。

 一个观测点是强影响点（influential observation），表明它对模型参数的估计产生的影响过大，非常不成比例。强影响点可以通过 Cook距离即Cook’s D统计量来鉴别。

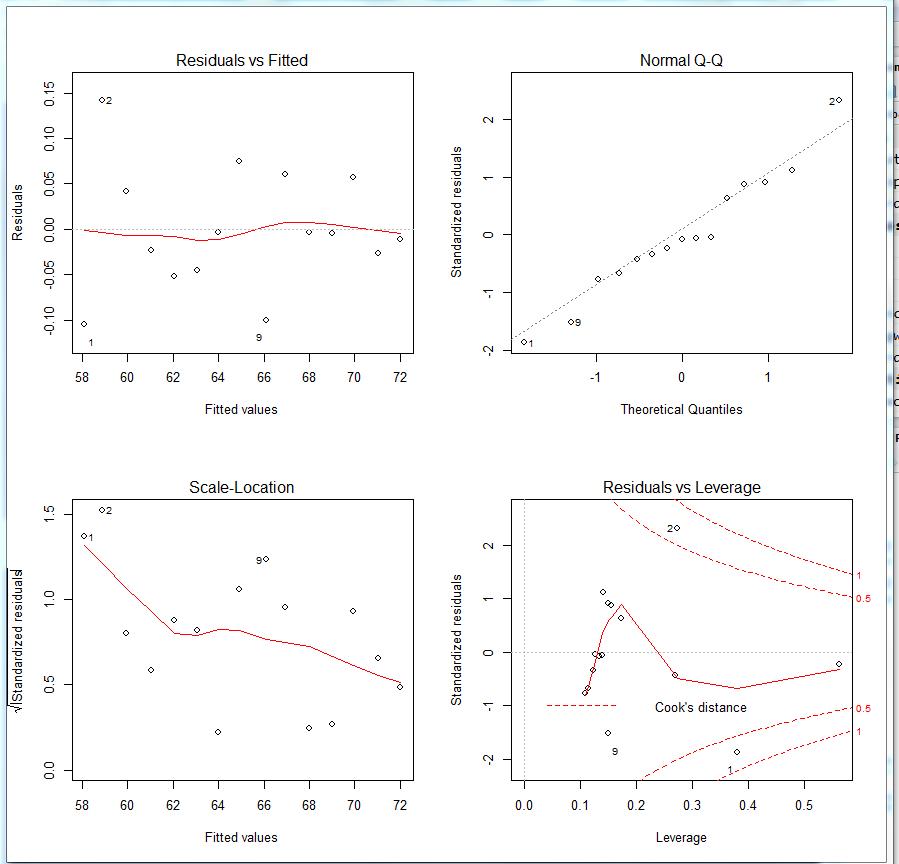
4.改进:

1. 删除离群点和强影响点

2. 变换—当y不服从正太分布时,

3. 方差不相同,变换Y的形式.

未完待续,

PPV原创文章,严禁转载. (文:@白加黑治感冒)

PPV课-国内领先的大数据学习社区（http://www.ppvke.com)